Dsalt Anillo ACT210087 (2022-2023)

The main goal of the project is to develop new computational algorithms to simulate seawater desalination processes. These advancements aim to provide technology developers with reliable simulations that support informed decision-making at a reduced cost.

As postdoctoral researcher during 2022 in the Anillo ACT210087 project, I focused on numerical methods with application on desalination processes. Water desalination is a problem often mentioned in the scientific community due to the increasing scarcity of available drinking water. A first approach, commonly used for the modelling of reverse-osmosis system in water filtration is to propose a coupled Navier-Stokes Diffusion model, where the Darcy’s law provides a relation between the permeability of the membrane and the amount of minerals in the water. One of the papers resulting from this research is (Carro et al., 2024), where we used Nitsche’s method for imposing the mineral-dependent permeability condition in a channel with saltwater flow.

Velocity streamlines (top panels) and concentration profiles (bottom panels) around the spacer in a cavity-type configuration.

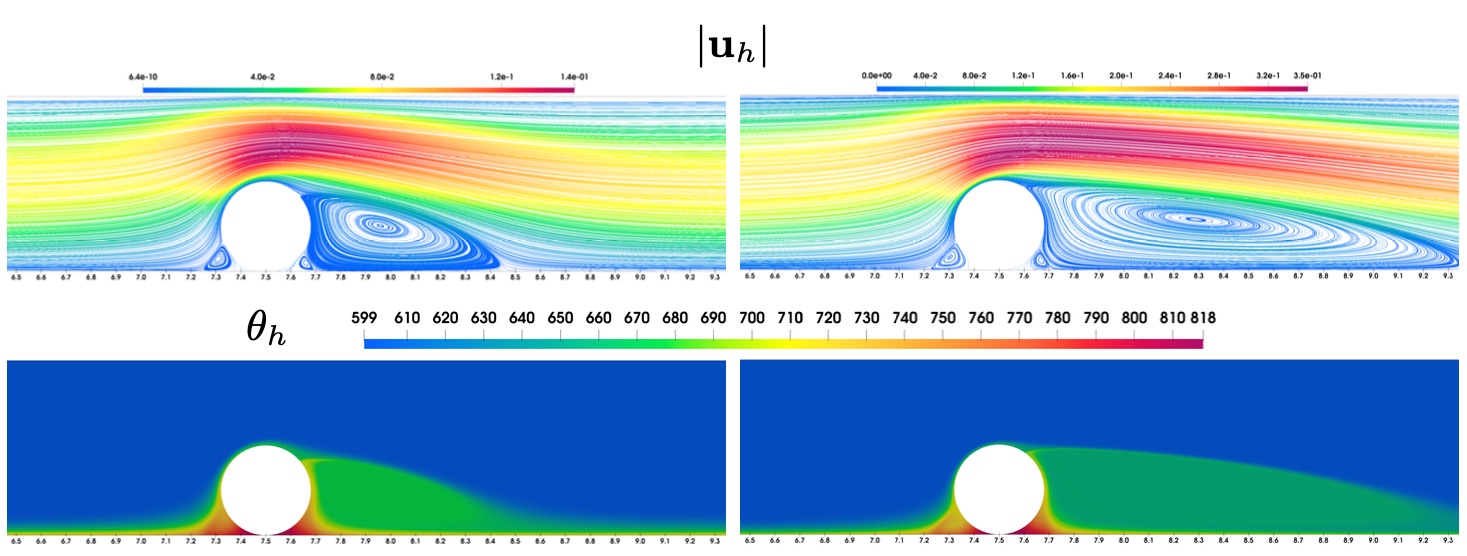
The project allowed me to do a research stay with Dr. Ricardo Ruiz-Baier at Monash University. I had the opportunity to study new software for solving partial differential equations. Specifically, I learned to use the Gridap software. This software has the capabilites of using the skeleton of the mesh and is specially useful when implementing Cut Finite element methods. Additionally, we investigated the use of a Lagrange multiplier to enforce specific conditions. However, particular attention is required to ensure accurate trace estimates for the analysis. As future research, we aim to explore the use of H(div)-conforming methods combined with a posteriori analysis to enhance information retrieval along the membrane. Moreover, poromechanics is being considered to model a coupled fluid–porous membrane–transport model.

Abstract In this article, we study a mathematical model that represents the concentration polarization and osmosis effects in a reverse osmosis cross-flow channel with dense membranes at some of its boundaries. The fluid is modeled using the Navier–Stokes equations and the solution-diffusion is used to impose the momentum balance on the membrane. The scheme consist of a conforming finite element method with the velocity–pressure formulation for the Navier–Stokes equations, together with a primal scheme for the convection–diffusion equations. The Nitsche’s method is used to impose the permeability condition across the membrane. Several numerical experiments are performed to show the robustness of the method. The resulting model accurately replicates the analytical models and predicts similar results to previous works. It is found that the submerged configuration has the highest permeate production, but also has the greatest pressure loss of all three configurations studied.

References